Puede llenar este formulario para recibir el link https://latam.m2iformacion.com/hackeando-humanos/
¿QUÉ ES LA ALFABETIZACIÓN DE DATOS?
La alfabetización de datos es la capacidad de leer, escribir y comunicar datos en contexto, incluida una comprensión de las fuentes de datos y construcciones, métodos analíticos y técnicas aplicadas, y la capacidad de describir el caso de uso aplicación y valor resultante.
PASO #1: ESTABLECER UNA LÍNEA DE BASE UTILIZANDO DATOS DE REGISTRO
Recopile datos de registro de sus herramientas de BI para comparar las tasas actuales de adopción y uso
PASO #2: IDENTIFIQUE GRUPOS QUE NO USAN DATOS
Utilizando los datos consolidades de logs, identificar grupos y usuarios con el mas bajo nivel de compromiso.
PASO #3: EVALUAR DATOS LITERATURA
Llevar a cabo una evaluación de la alfabetización de datos. Identifica necesidades únicas de grupos con diferentes niveles de habilidad.
PASO #4: IDENTIFIQUE CAMPEONES EN DATOS
Identifique usuarios avanzados y departamentos altamente calificados. Reclutar campeones de datos.
PASO #5: CREAR RECURSOS EDUCACIONALES
Entreviste campeones, grabe videos sobre mejores prácticas, crear casos de uso, consejos y trucos que ayudarán a educar otros grupos.
PASO #6: LANZAR UNA CAMPANA EDUCATIVA.
Enseñe y distribuya los recursos educacionales a lo largo de la organización.
PASO #7: MEDIR EL PROGRESO: EJECUTAR Y REPETIR.
Mida los cambios y adopciones sobre el rendimiento del negocio. Realice otra evaluación de habilidades.
Los algoritmos y el software de Dongarra impulsaron el crecimiento de la computación de alto rendimiento y tuvieron un impacto significativo en muchas áreas de la ciencia computacional, desde la IA hasta los gráficos por ordenador
Nueva York, NY, 30 de marzo de 2022 – ACM, la Asociación para la Maquinaria Informática, ha nombrado hoy a Jack J. Dongarra ganador del Premio ACM A.M. Turing 2021 por sus contribuciones pioneras a los algoritmos numéricos y las bibliotecas que permitieron que el software de computación de alto rendimiento siguiera el ritmo de las mejoras exponenciales del hardware durante más de cuatro décadas. Dongarra es profesor distinguido de informática en el Departamento de Ingeniería Eléctrica e Informática de la Universidad de Tennessee. También es miembro del Oak Ridge National Laboratory y de la Universidad de Manchester.
El premio ACM A.M. Turing, a menudo a denominado «Premio Nobel de la Informática», está dotado con un millón de dólares y cuenta con el apoyo financiero de Google, Inc. Lleva el nombre de Alan M. Turing, el matemático británico que articuló los fundamentos matemáticos y los límites de la informática.
Dongarra ha liderado el mundo de la computación de alto rendimiento gracias a sus contribuciones a los algoritmos numéricos eficientes para las operaciones de álgebra lineal, los mecanismos de programación de la computación paralela y las herramientas de evaluación del rendimiento. Durante casi cuarenta años, la Ley de Moore produjo un crecimiento exponencial del rendimiento del hardware. Durante ese mismo tiempo, mientras la mayor parte del software no pudo seguir el ritmo de estos avances del hardware, el software numérico de alto rendimiento sí lo hizo, en gran parte gracias a los algoritmos, las técnicas de optimización y las implementaciones de software de calidad de producción de Dongarra.
Estas contribuciones establecieron un marco a partir del cual los científicos e ingenieros hicieron importantes descubrimientos e innovaciones que cambiaron el juego en áreas como el análisis de grandes datos, la salud, la energía renovable, la predicción del tiempo, la genómica y la economía, por nombrar algunas. El trabajo de Dongarra también ayudó a facilitar los avances en la arquitectura de los ordenadores y apoyó las revoluciones en los gráficos por ordenador y el aprendizaje profundo.
La mayor contribución de Dongarra fue la creación de bibliotecas y estándares de software de código abierto que emplean el álgebra lineal como un lenguaje intermedio que puede ser utilizado por una amplia variedad de aplicaciones. Estas bibliotecas se han escrito para procesadores individuales, ordenadores paralelos, nodos multinúcleo y múltiples GPU por nodo. Las bibliotecas de Dongarra también introdujeron muchas innovaciones importantes, como el autoajuste, la aritmética de precisión mixta y los cálculos por lotes.
Como principal embajador de la computación de alto rendimiento, Dongarra se encargó de convencer a los proveedores de hardware para que optimizaran estos métodos y a los desarrolladores de software para que utilizaran sus bibliotecas de código abierto en su trabajo. En última instancia, estos esfuerzos dieron lugar a que las bibliotecas de software basadas en el álgebra lineal lograran una adopción casi universal para la computación científica y de ingeniería de alto rendimiento en máquinas que van desde los ordenadores portátiles hasta los superordenadores más rápidos del mundo. Estas bibliotecas fueron esenciales para el crecimiento del campo, permitiendo que ordenadores cada vez más potentes resolvieran problemas computacionales difíciles.
«Los superordenadores más rápidos de hoy en día acaparan los titulares de los medios de comunicación y despiertan el interés del público al realizar hazañas alucinantes de un cuatrillón de cálculos en un segundo», explica la presidenta de la ACM, Gabriele Kotsis. «Pero más allá del comprensible interés por la superación de nuevos récords, la computación de alto rendimiento ha sido un importante instrumento de descubrimiento científico. Las innovaciones de la computación de alto rendimiento también se han extendido a muchas áreas diferentes de la informática y han hecho avanzar todo nuestro campo». Jack Dongarra desempeñó un papel fundamental en la dirección de la exitosa trayectoria de este campo. Su trabajo pionero se remonta a 1979 y sigue siendo uno de los líderes más destacados y comprometidos de la comunidad de la HPC. Su carrera ejemplifica sin duda el reconocimiento del Premio Turing a las «grandes contribuciones de importancia duradera»».
«El trabajo de Jack Dongarra ha cambiado fundamentalmente y ha hecho avanzar la computación científica», dijo Jeff Dean, Senior Fellow de Google y SVP de Google Research y Google Health. «Su profundo e importante trabajo en el núcleo de las bibliotecas numéricas más utilizadas del mundo subyace en todas las áreas de la computación científica, ayudando a avanzar en todo, desde el descubrimiento de fármacos hasta la predicción del tiempo, la ingeniería aeroespacial y docenas de campos más, y su profundo enfoque en la caracterización del rendimiento de una amplia gama de ordenadores ha llevado a importantes avances en las arquitecturas de los ordenadores que son muy adecuadas para los cálculos numéricos.»
Dongarra recibirá formalmente el premio ACM A.M. Turing en el banquete anual de premios de la ACM, que este año se celebrará el sábado 11 de junio en el Hotel Palace de San Francisco
CONTRIBUCIONES TÉCNICAS SELECTAS
Durante más de cuatro décadas, Dongarra ha sido el principal implementador o investigador de muchas bibliotecas como LINPACK, BLAS, LAPACK, ScaLAPACK, PLASMA, MAGMA y SLATE. Estas librerías se han escrito para procesadores individuales, ordenadores paralelos, nodos multinúcleo y múltiples GPU por nodo. Sus bibliotecas de software se utilizan, prácticamente de forma universal, para el cálculo científico y de ingeniería de alto rendimiento en máquinas que van desde los ordenadores portátiles hasta los superordenadores más rápidos del mundo.
Estas bibliotecas incorporan numerosas innovaciones técnicas de gran calado, como: Autotuning: a través de su proyecto ATLAS, premiado en la Conferencia de Supercomputación de 2016, Dongarra fue pionero en la búsqueda automática de parámetros algorítmicos que producen núcleos de álgebra lineal de eficiencia casi óptima, a menudo superando los códigos suministrados por los proveedores.
Aritmética de precisión mixta: En su artículo de la Conferencia de Supercomputación de 2006, «Exploiting the Performance of 32 bit Floating Point Arithmetic in Obtaining 64 bit Accuracy», Dongarra fue pionero en el aprovechamiento de las múltiples precisiones de la aritmética de punto flotante para ofrecer soluciones precisas con mayor rapidez. Este trabajo se ha convertido en un elemento fundamental en las aplicaciones de aprendizaje automático, como se ha demostrado recientemente en la prueba de referencia HPL-AI, que ha alcanzado niveles de rendimiento sin precedentes en los mejores superordenadores del mundo.
Cálculos por lotes: Dongarra fue pionero en el paradigma de dividir los cálculos de grandes matrices densas, que se utilizan habitualmente en simulaciones, modelado y análisis de datos, en muchos cálculos de tareas más pequeñas en bloques que pueden calcularse de forma independiente y concurrente. Basándose en su artículo de 2016, «Performance, design, and autotuning of batched GEMM for GPUs», Dongarra dirigió el desarrollo del estándar Batched BLAS para este tipo de cálculos, y también aparecen en las bibliotecas de software MAGMA y SLATE.
Dongarra ha colaborado a nivel internacional con muchas personas en los esfuerzos mencionados, siempre en el papel de impulsor de la innovación desarrollando continuamente nuevas técnicas para maximizar el rendimiento y la portabilidad, al tiempo que se mantienen resultados numéricamente fiables utilizando las técnicas más avanzadas. Otros ejemplos de su liderazgo son la interfaz de paso de mensajes (MPI), el estándar de facto para el paso de mensajes portátil en arquitecturas de computación paralela, y la API de rendimiento (PAPI), que proporciona una interfaz que permite la recopilación y síntesis del rendimiento de los componentes de un sistema heterogéneo. Los estándares que ayudó a crear, como MPI, el LINPACK Benchmark y la lista Top500 de superordenadores, sustentan tareas computacionales que van desde la predicción del tiempo hasta el cambio climático, pasando por el análisis de datos de experimentos de física a gran escala.
Antecedentes biográficos
Jack J. Dongarra es profesor distinguido de la Universidad de Tennessee y miembro distinguido del personal de investigación del Laboratorio Nacional de Oak Ridge desde 1989. También ha sido becario Turing en la Universidad de Manchester (Reino Unido) desde 2007. Dongarra se licenció en Matemáticas por la Universidad Estatal de Chicago, obtuvo un máster en Informática por el Instituto Tecnológico de Illinois y un doctorado en Matemáticas Aplicadas por la Universidad de Nuevo México.
Dongarra ha recibido, entre otros, el premio IEEE Computer Pioneer, el premio SIAM/ACM en Ciencia e Ingeniería Computacional y el premio ACM/IEEE Ken Kennedy. Es miembro de la ACM, el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE), la Sociedad de Matemáticas Industriales y Aplicadas (SIAM), la Asociación Americana para el Avance de la Ciencia (AAAS), la Conferencia Internacional de Supercomputación (ISC) y el Instituto Internacional de Ingeniería y Tecnología (IETI). Es miembro de la Academia Nacional de Ingeniería y miembro extranjero de la Real Sociedad Británica.
Acerca del Premio A.M. Turing de la ACM
El Premio A.M. Turing lleva el nombre de Alan M. Turing, el matemático británico que articuló los fundamentos matemáticos y los límites de la informática, y que fue un colaborador clave en el criptoanálisis aliado de la clave Enigma durante la Segunda Guerra Mundial. Desde su creación en 1966, el Premio Turing ha honrado a los científicos e ingenieros informáticos que crearon los sistemas y los fundamentos teóricos subyacentes que han impulsado la industria de la tecnología de la información.
Acerca de ACM
ACM, la Association for Computing Machinery, es la mayor sociedad educativa y científica de informática del mundo, que une a educadores, investigadores y profesionales para inspirar el diálogo, compartir recursos y abordar los retos de este campo. ACM refuerza la voz colectiva de la profesión informática a través de un fuerte liderazgo, la promoción de los más altos estándares y el reconocimiento de la excelencia técnica. La ACM apoya el crecimiento profesional de sus miembros ofreciéndoles oportunidades de aprendizaje permanente, desarrollo de su carrera y creación de redes profesionales.
La ciencia busca las leyes básicas de la naturaleza. Las matemáticas buscan nuevos teoremas que se basen en los antiguos. La ingeniería construye sistemas para resolver las necesidades humanas. Las tres disciplinas son interdependientes pero distintas. Es muy raro que una persona haga simultáneamente contribuciones fundamentales a las tres, pero Claude Shannon era una persona rara.
A pesar de ser el protagonista del reciente documental The Bit Player -y de que su trabajo y filosofía de investigación han inspirado mi propia carrera- Shannon no es precisamente un nombre conocido. Nunca ganó un Premio Nobel y no era una celebridad como Albert Einstein o Richard Feynman, ni antes ni después de su muerte en 2001. Pero hace más de 70 años, en un único e innovador artículo, sentó las bases de toda la infraestructura de comunicación que subyace a la era moderna de la información.
Shannon nació en Gaylord, Michigan, en 1916, hijo de un empresario local y una profesora. Tras licenciarse en ingeniería eléctrica y matemáticas por la Universidad de Michigan, escribió una tesis de máster en el Instituto Tecnológico de Massachusetts que aplicaba una disciplina matemática llamada álgebra de Boole al análisis y la síntesis de circuitos de conmutación. Fue un trabajo transformador, que convirtió el diseño de circuitos de un arte a una ciencia, y ahora se considera que fue el punto de partida del diseño de circuitos digitales.
A continuación, Shannon puso la mira en un objetivo aún mayor: la comunicación.
Claude Shannon escribió una tesis de maestría que puso en marcha el diseño de circuitos digitales, y una década más tarde escribió su documento seminal sobre la teoría de la información, «Una teoría matemática de la comunicación».
La comunicación es una de las necesidades humanas más básicas. Desde las señales de humo hasta las palomas mensajeras, pasando por el teléfono y la televisión, el ser humano siempre ha buscado métodos que le permitieran comunicarse más lejos, más rápido y de forma más fiable. Pero la ingeniería de los sistemas de comunicación siempre estuvo ligada a la fuente y el medio físico específicos. Shannon, en cambio, se preguntó: «¿Existe una gran teoría unificada para la comunicación?». En una carta de 1939 a su mentor, Vannevar Bush, Shannon esbozó algunas de sus ideas iniciales sobre «las propiedades fundamentales de los sistemas generales para la transmisión de inteligencia». Tras trabajar en el problema durante una década, Shannon publicó finalmente su obra maestra en 1948: «Una teoría matemática de la comunicación».
El núcleo de su teoría es un modelo sencillo pero muy general de comunicación: Un transmisor codifica la información en una señal, que es corrompida por el ruido y decodificada por el receptor. A pesar de su simplicidad, el modelo de Shannon incorpora dos ideas clave: aislar las fuentes de información y de ruido del sistema de comunicación que se va a diseñar, y modelar ambas fuentes de forma probabilística. Imaginó que la fuente de información generaba uno de los muchos mensajes posibles para comunicar, cada uno de los cuales tenía una determinada probabilidad. El ruido probabilístico añadía más aleatoriedad para que el receptor pudiera desentrañar.
Antes de Shannon, el problema de la comunicación se consideraba principalmente un problema de reconstrucción de señales deterministas: cómo transformar una señal recibida, distorsionada por el medio físico, para reconstruir el original con la mayor precisión posible. La genialidad de Shannon reside en su observación de que la clave de la comunicación es la incertidumbre. Al fin y al cabo, si supiera de antemano lo que le voy a decir en esta columna, ¿qué sentido tendría escribirla?
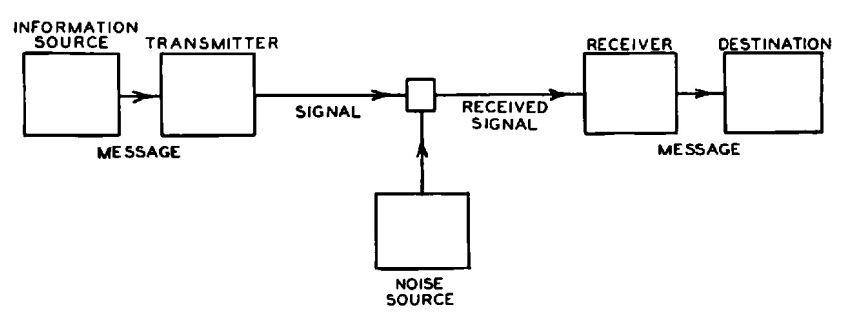
Diagrama esquemático del modelo de comunicación de Shannon, extraído de su documento.
Esta única observación desplazó el problema de la comunicación de lo físico a lo abstracto, permitiendo a Shannon modelar la incertidumbre utilizando la probabilidad. Esto supuso un shock total para los ingenieros de comunicación de la época.
En este marco de incertidumbre y probabilidad, Shannon se propuso determinar sistemáticamente el límite fundamental de la comunicación. Su respuesta se divide en tres partes. El concepto de «bit» de información, utilizado por Shannon como unidad básica de incertidumbre, desempeña un papel fundamental en las tres. Un bit, que es una abreviatura de «dígito binario», puede ser un 1 o un 0, y el documento de Shannon es el primero en utilizar la palabra (aunque él dijo que el matemático John Tukey la utilizó primero en un memorando).
En primer lugar, Shannon ideó una fórmula para el número mínimo de bits por segundo para representar la información, un número que denominó tasa de entropía, H. Este número cuantifica la incertidumbre que supone determinar qué mensaje generará la fuente. Cuanto menor sea la tasa de entropía, menor será la incertidumbre y, por tanto, más fácil será comprimir el mensaje en algo más corto. Por ejemplo, enviar mensajes de texto a un ritmo de 100 letras inglesas por minuto significa enviar uno de los 26100 mensajes posibles cada minuto, cada uno representado por una secuencia de 100 letras. Se podrían codificar todas estas posibilidades en 470 bits, ya que 2470 ≈ 26100. Si las secuencias fueran igualmente probables, la fórmula de Shannon diría que la tasa de entropía es efectivamente de 470 bits por minuto. En realidad, algunas secuencias son mucho más probables que otras, y la tasa de entropía es mucho menor, lo que permite una mayor compresión.
En segundo lugar, proporcionó una fórmula para el número máximo de bits por segundo que pueden comunicarse de forma fiable frente al ruido, que denominó capacidad del sistema, C. Se trata de la velocidad máxima a la que el receptor puede resolver la incertidumbre del mensaje, lo que la convierte en el límite de velocidad de la comunicación.
Por último, demostró que la comunicación fiable de la información de la fuente frente al ruido es posible si y sólo si H < C. Así, la información es como el agua: Si el caudal es inferior a la capacidad de la tubería, la corriente pasa de forma fiable.
Aunque se trata de una teoría de la comunicación, es, al mismo tiempo, una teoría de cómo se produce y transfiere la información: una teoría de la información. Por eso Shannon es considerado hoy «el padre de la teoría de la información».
Sus teoremas condujeron a algunas conclusiones contraintuitivas. Supongamos que usted está hablando en un lugar muy ruidoso. ¿Cuál es la mejor manera de asegurarse de que su mensaje llega? ¿Quizás repetirlo muchas veces? Ése es sin duda el primer instinto de cualquiera en un restaurante ruidoso, pero resulta que no es muy eficaz. Seguro que cuantas más veces te repitas, más fiable será la comunicación. Pero has sacrificado la velocidad por la fiabilidad. Shannon nos mostró que podemos hacerlo mucho mejor. Repetir un mensaje es un ejemplo de utilizar un código para transmitir un mensaje, y utilizando códigos diferentes y más sofisticados, se puede comunicar rápidamente – hasta el límite de velocidad, C – manteniendo cualquier grado de fiabilidad.
Otra conclusión inesperada que se desprende de la teoría de Shannon es que, sea cual sea la naturaleza de la información (un soneto de Shakespeare, una grabación de la Quinta Sinfonía de Beethoven o una película de Kurosawa), siempre es más eficaz codificarla en bits antes de transmitirla. Así, en un sistema de radio, por ejemplo, aunque tanto el sonido inicial como la señal electromagnética enviada por el aire son formas de onda analógicas, los teoremas de Shannon implican que lo óptimo es digitalizar primero la onda sonora en bits, y luego mapear esos bits en la onda electromagnética. Este sorprendente resultado es la piedra angular de la moderna era de la información digital, en la que el bit reina como moneda universal de la información.
Shannon también tenía un lado lúdico, que a menudo llevaba a su trabajo. Aquí, posa con un laberinto que construyó para un ratón electrónico, llamado Theseus.
La teoría general de la comunicación de Shannon es tan natural que es como si hubiera descubierto las leyes de la comunicación del universo, en lugar de inventarlas. Su teoría es tan fundamental como las leyes físicas de la naturaleza. En ese sentido, era un científico.
Shannon inventó nuevas matemáticas para describir las leyes de la comunicación. Introdujo nuevas ideas, como la tasa de entropía de un modelo probabilístico, que se han aplicado en ramas matemáticas de gran alcance, como la teoría ergódica, el estudio del comportamiento a largo plazo de los sistemas dinámicos. En ese sentido, Shannon era un matemático.
Pero, sobre todo, Shannon era un ingeniero. Su teoría estaba motivada por problemas prácticos de ingeniería. Y aunque era esotérica para los ingenieros de su época, la teoría de Shannon se ha convertido en el marco estándar en el que se basan todos los sistemas de comunicación modernos: ópticos, submarinos e incluso interplanetarios. Personalmente, he tenido la suerte de formar parte de un esfuerzo mundial por aplicar y ampliar la teoría de Shannon a la comunicación inalámbrica, aumentando la velocidad de las comunicaciones en dos órdenes de magnitud a lo largo de múltiples generaciones de estándares. De hecho, el estándar 5G que se está implantando actualmente utiliza no uno, sino dos códigos prácticos probados para alcanzar el límite de velocidad de Shannon.
Aunque Shannon murió en 2001, su legado sigue vivo en la tecnología que conforma nuestro mundo moderno y en los dispositivos que creó, como este autobús teledirigido
Shannon descubrió la base de todo esto hace más de 70 años. ¿Cómo lo hizo? Centrándose implacablemente en la característica esencial de un problema e ignorando todos los demás aspectos. La simplicidad de su modelo de comunicación es una buena ilustración de este estilo. También sabía centrarse en lo que es posible, más que en lo que es inmediatamente práctico.
El trabajo de Shannon ilustra el verdadero papel de la ciencia de alto nivel. Cuando empecé a estudiar en la universidad, mi asesor me dijo que el mejor trabajo era podar el árbol del conocimiento, en lugar de hacerlo crecer. Entonces no sabía qué pensar de este mensaje; siempre pensé que mi trabajo como investigador era añadir mis propias ramitas. Pero a lo largo de mi carrera, cuando tuve la oportunidad de aplicar esta filosofía en mi propio trabajo, empecé a entenderlo.
Cuando Shannon empezó a estudiar la comunicación, los ingenieros ya tenían una gran colección de técnicas. Fue su trabajo de unificación el que podó todas estas ramitas de conocimiento en un único árbol coherente y encantador, que ha dado sus frutos a generaciones de científicos, matemáticos e ingenieros.
